Have you ever gazed up at a towering skyscraper and wondered how architects design such complex structures? Or perhaps marveled at the intricate patterns in a honeycomb and questioned the mathematics behind its creation? Geometry, the study of shapes, sizes, and positions, provides the answers to these questions and more. It’s a fundamental branch of mathematics that permeates our world, from the smallest atoms to the vast expanse of the cosmos. Understanding the defined terms in geometry is like unlocking a secret code, allowing us to decipher the patterns and relationships that govern the physical world around us.
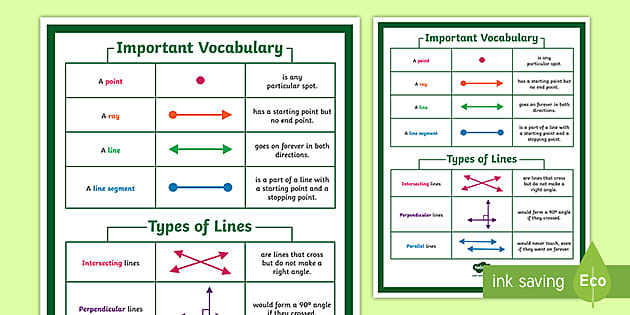
Image: www.twinkl.it
Let’s embark on an exciting journey into the realm of geometry, where we’ll explore some essential definitions that form the bedrock of this fascinating subject. From points and lines to angles and shapes, we’ll uncover the language that mathematicians use to describe and analyze the visual world.
The Building Blocks of Geometry: Points, Lines, and Planes
Imagine a single dot on a piece of paper. That tiny dot, representing a precise location, is what we call a point. A point has no dimension, meaning it doesn’t have any length, width, or height. It’s simply a location in space. Now, envision drawing a straight path connecting two points. This path, extending infinitely in both directions, is called a line. A line has only one dimension – length. Lines are fundamental in geometry, forming the basis for constructing more complex shapes.
Next, imagine extending the line upwards and downwards, like a sheet of paper stretched infinitely. This infinite flat surface is called a plane. A plane has two dimensions – length and width. Points, lines, and planes are the basic building blocks of geometry, and understanding their properties is crucial to grasp more complex concepts.
Dimensions and Shapes: Unveiling the Geometry of Our World
Think of a pencil. It has length, but no width or depth. That’s a one-dimensional object. Now imagine a sheet of paper. It has both length and width but no depth. This is a two-dimensional object. Finally, consider your favorite coffee mug. It has length, width, and depth. This is a three-dimensional object.
The number of dimensions an object occupies determines its shape. One-dimensional objects are simply lines. Two-dimensional objects are flat shapes, like circles, squares, and triangles. Three-dimensional objects have volume, like cubes, spheres, and pyramids.
The Language of Angles: Measuring Rotations
Imagine the arms of a clock. As the clock ticks, the hands rotate, forming different angles. An angle is the measure of the rotation between two lines that share a common endpoint, called the vertex. Angles are measured in degrees (°) or radians. A full circle encompasses 360 degrees or 2π radians.
There are different types of angles, each with specific properties. A right angle measures exactly 90 degrees, forming a perfect corner. An acute angle is less than 90 degrees, while an obtuse angle is greater than 90 degrees. These angles play vital roles in classifying triangles and other shapes.
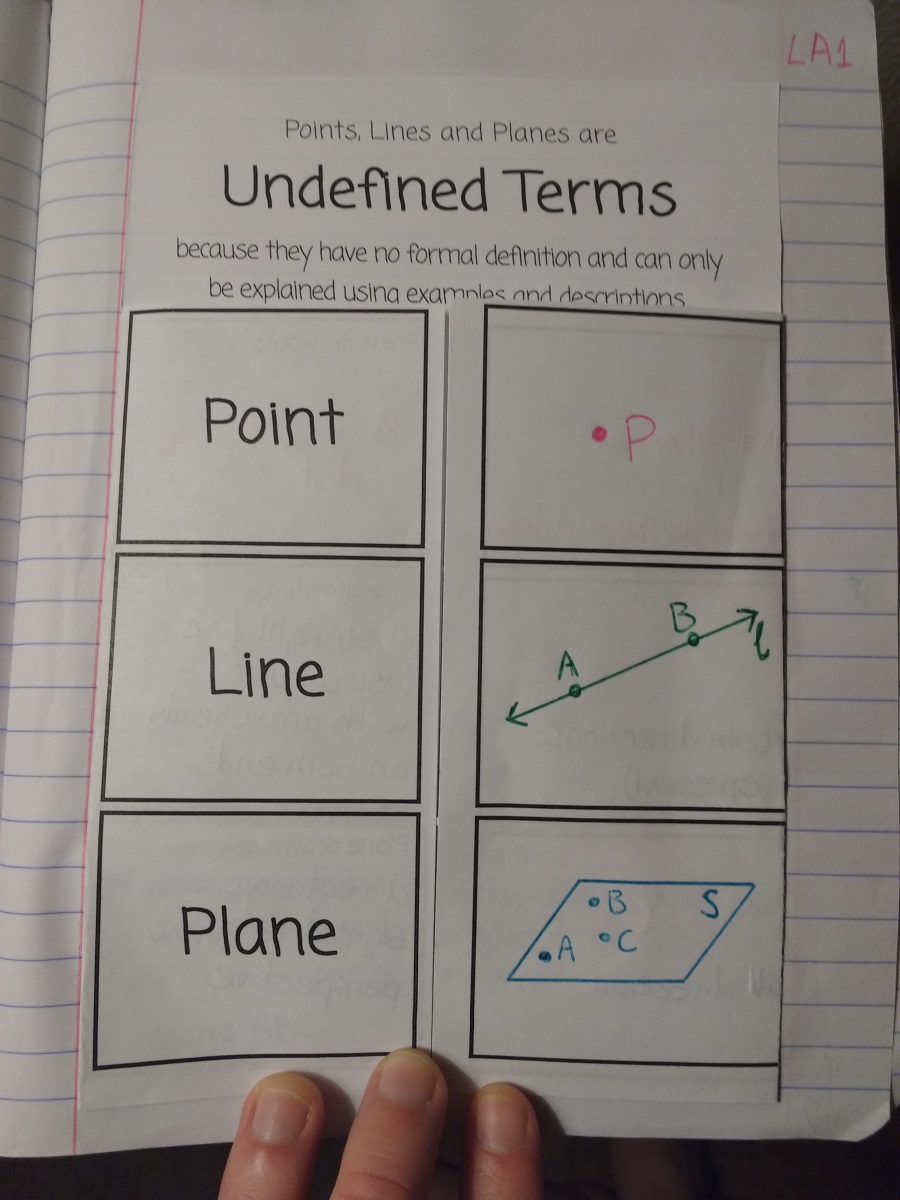
Image: www.primefactorisation.com
Triangles: The Foundation of Geometric Shapes
Triangles are the most fundamental polygons in geometry, with three sides and three angles. Their stability and versatility make them essential in construction, engineering, and architecture. There are many types of triangles, each named after its angle measures or side lengths.
A scalene triangle has all sides of different lengths, while an isosceles triangle has two sides of equal length. An equilateral triangle has all sides equal, and all angles measure 60 degrees. A right triangle has one angle that measures 90 degrees, forming a right angle.
Exploring Geometric Shapes: Beyond the Triangle
Triangles are just the beginning. Geometry encompasses a vast array of shapes, each with unique properties and applications. A quadrilateral is any four-sided polygon, including squares, rectangles, parallelograms, and trapezoids.
Circles, defined as the set of all points equidistant from a central point, are essential in mathematics, physics, and engineering. Polygons are closed shapes made up of straight line segments, with a variety of classifications based on the number of sides and angles.
Constructions and Theorems: The Logic of Geometry
Geometry is not just about shapes; it’s also about the relationships between them. This is where geometric constructions and theorems come into play. Geometric constructions involve drawing and manipulating geometric figures using only a compass and a straightedge, following specific rules.
Theorems are statements that have been proven to be true through logical reasoning and deductions, often using axioms and postulates. For example, the Pythagorean Theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
Geometry’s Applications: Shaping Our World
The principles of geometry are not confined to textbooks; they have far-reaching applications in our daily lives. Architects use geometric concepts to design buildings, bridges, and other structures. Engineers apply geometry in the development of airplanes, cars, and other technologies.
Cartographers use geometry to create maps, while scientists leverage it to model complex natural phenomena. Geometry is a crucial tool for understanding the universe, from the intricate patterns in nature to the vast expanse of the cosmos.
Examples Of Defined Terms In Geometry
Embrace the Power of Geometric Thinking
Learning geometry is about more than just memorizing definitions and formulas; it’s about cultivating a way of thinking. By understanding the principles of geometry, we can analyze and interpret the world around us more effectively. We can uncover the hidden patterns in nature, appreciate the beauty of geometric art, and even develop innovative solutions to complex problems.
Start your journey into the world of geometry by exploring the definitions and concepts presented here. And remember, geometry is not just a subject; it’s a language we can use to communicate and create. So, go ahead, unlock the secrets of geometry, and see how it shapes your perspective on the world.






